Một vùng biển được mô hình hoá thành lưới ô vuông kích thước ~n \times m~.

Tàu ngầm gồm ~k~ khoang, có thể coi như một hình chữ nhật kích thước ~1 \times k~ (tức là một đoạn thẳng dài ~k~ ô), và có thể đặt theo một trong hai hướng:

• Nằm ngang (chiếm ~k~ ô liên tiếp trên cùng một hàng),
• Nằm dọc (chiếm ~k~ ô liên tiếp trên cùng một cột).

Một quả bom chống tàu ngầm đã được thả xuống ô ~(x,y)~ và chắc chắn đã phá hủy một khoang của tàu ngầm, tức là ô ~(x,y)~ thuộc tàu ngầm.

Để đánh đắm tàu ngầm cần phá hủy tất cả ~k~ khoang. Mỗi quả bom thả vào một ô sẽ phá hủy khoang nếu ô đó thuộc tàu ngầm.

Hãy xác định số lượng bom ít nhất cần thả thêm (không tính quả bom đã thả ở ~(x,y)~) để chắc chắn đánh đắm tàu ngầm, trong trường hợp ta không biết chính xác vị trí và hướng của tàu ngầm ngoài việc nó dài ~k~ và đi qua ~(x,y)~.

Yêu cầu

Tìm số nguyên nhỏ nhất ~B~ sao cho có thể chọn thêm ~B~ ô để thả bom, đảm bảo rằng dù tàu ngầm đặt ở đâu (hợp lệ trong lưới và đi qua ~(x,y)~), thì tất cả ~k~ ô của tàu ngầm đều bị nổ bom trúng.

Dữ liệu

• Dòng 1: hai số nguyên ~n~, ~m~.
• Dòng 2: hai số nguyên ~x~, ~y~.
• Dòng 3: số nguyên ~k~.

Kết quả

In ra một số nguyên — số bom ít nhất cần thả thêm.

Ví dụ

Ví dụ 1

Input

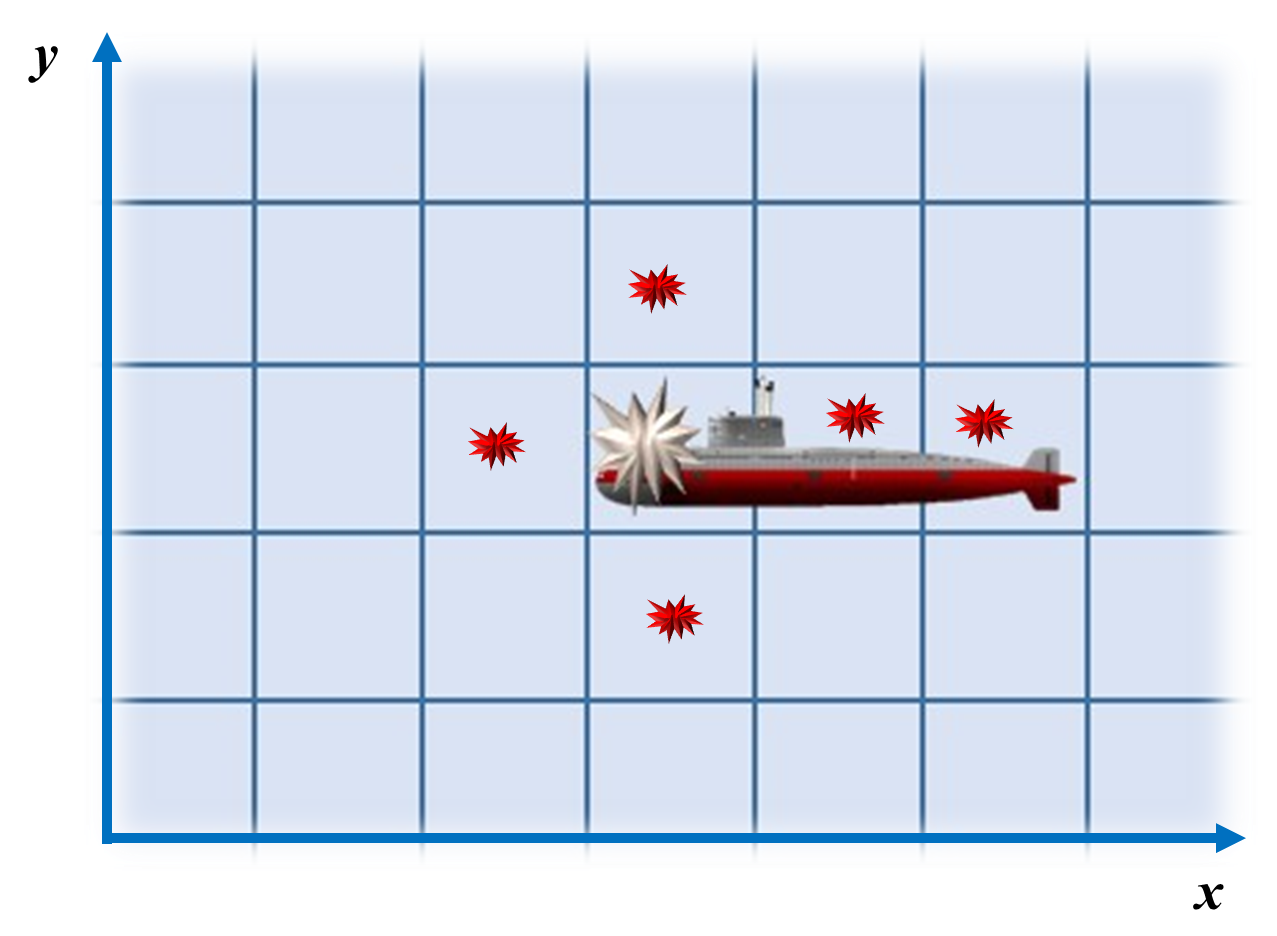
7 5
4 3
3

Output

5

Giải thích

Ví dụ 1

Tàu ngầm dài ~3~ ô, có thể nằm ngang hoặc dọc và chắc chắn đi qua ô ~(4,3)~. Để chắc chắn đánh đắm tàu ngầm trong mọi cách đặt hợp lệ, cần thả thêm tối thiểu ~5~ bom (ngoài quả đã thả tại ~(4,3)~).

Ràng buộc và chấm điểm

Ràng buộc

• ~1 \le n, m \le 20~
• ~1 \le x \le n~, ~1 \le y \le m~
• ~1 \le k \le \max{n,m}~