Một tổ hợp nghiên cứu đại dương gồm ~n~ phòng ngầm dưới nước và ~n-1~ hành lang nối các phòng. Mỗi hành lang cho phép di chuyển hai chiều. Từ bất kỳ phòng nào cũng có thể đi tới bất kỳ phòng nào khác, tức hệ thống có dạng cây.

Với mỗi hành lang thứ ~i~, nó nối hai phòng ~a_i~ và ~b_i~, có:

• độ dài ~d_i~ (thời gian đi qua hành lang đúng bằng ~d_i~),
• và chỉ chịu được đến thời điểm ~t_i~ (tính từ lúc bắt đầu động đất), sau đó hành lang sụp.

Khi có báo động, nhân viên tại một phòng phải di chuyển về một phòng nổi để sơ tán. Phòng nổi được định nghĩa là phòng có đúng một hành lang nối (tức bậc ~1~) khi ~n>1~. Nếu ~n=1~ thì phòng duy nhất cũng được coi là phòng nổi.

Quy tắc an toàn:

• Thời gian đi qua một phòng là không đáng kể.
• Nếu đang ở trong hành lang mà hành lang sụp thì không thể cứu được.
• Nếu đến được phòng tiếp theo đúng lúc hành lang sụp (tức là kết thúc việc đi qua tại thời điểm ~t_i~) thì vẫn an toàn.
• Hành lang đã sụp thì không thể đi qua nữa.

Một số phòng có thể không kịp thoát tới bất kỳ phòng nổi nào; các phòng đó phải thiết kế lại.

Yêu cầu

Hãy xác định theo thiết kế hiện tại có bao nhiêu phòng không cần thiết kế lại, tức là số phòng mà nhân viên xuất phát từ đó có thể đi tới ít nhất một phòng nổi an toàn (đi ngay lập tức, theo các hành lang trên cây).

Dữ liệu

• Dòng đầu chứa số nguyên ~n~ (~1 \le n \le 10^5~).

• ~n-1~ dòng tiếp theo, dòng thứ ~i~ chứa 4 số nguyên ~a_i, b_i, d_i, t_i~:

  • ~1 \le a_i, b_i \le n~, ~a_i \ne b_i~
  • ~1 \le d_i \le 10^4~
  • ~1 \le t_i \le 10^9~

Kết quả

In ra một số nguyên: số lượng phòng không đòi hỏi phải thiết kế lại.

Ví dụ

Ví dụ 1

Input

7
1 6 4 5
3 4 3 3
5 1 4 4
7 4 2 4
2 4 4 6
3 1 3 4

Output

6

Giải thích

Ví dụ 1

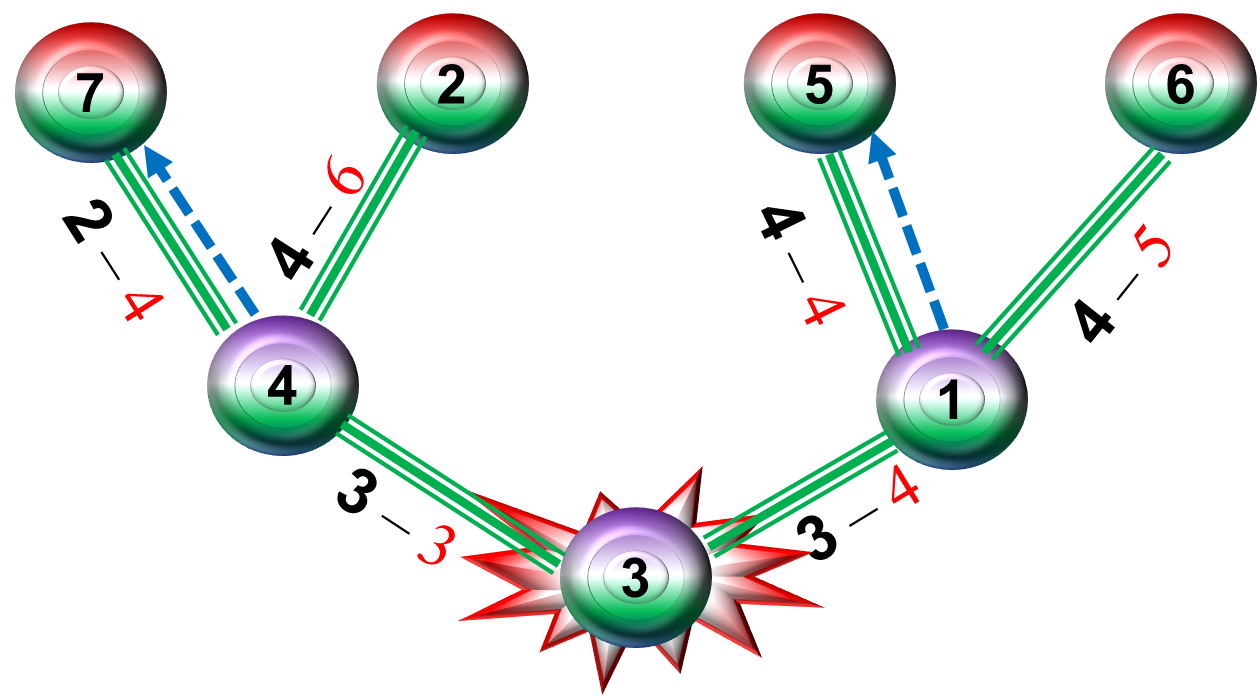
Có đúng ~6~ phòng mà từ đó tồn tại một đường đi tới một phòng nổi sao cho với mỗi hành lang trên đường đi, thời điểm kết thúc việc đi qua hành lang đó không vượt quá ~t_i~.

Ràng buộc và chấm điểm

Ràng buộc

• ~1 \le n \le 10^5~
• Cây có ~n~ đỉnh, ~n-1~ cạnh
• ~1 \le d_i \le 10^4~, ~1 \le t_i \le 10^9~