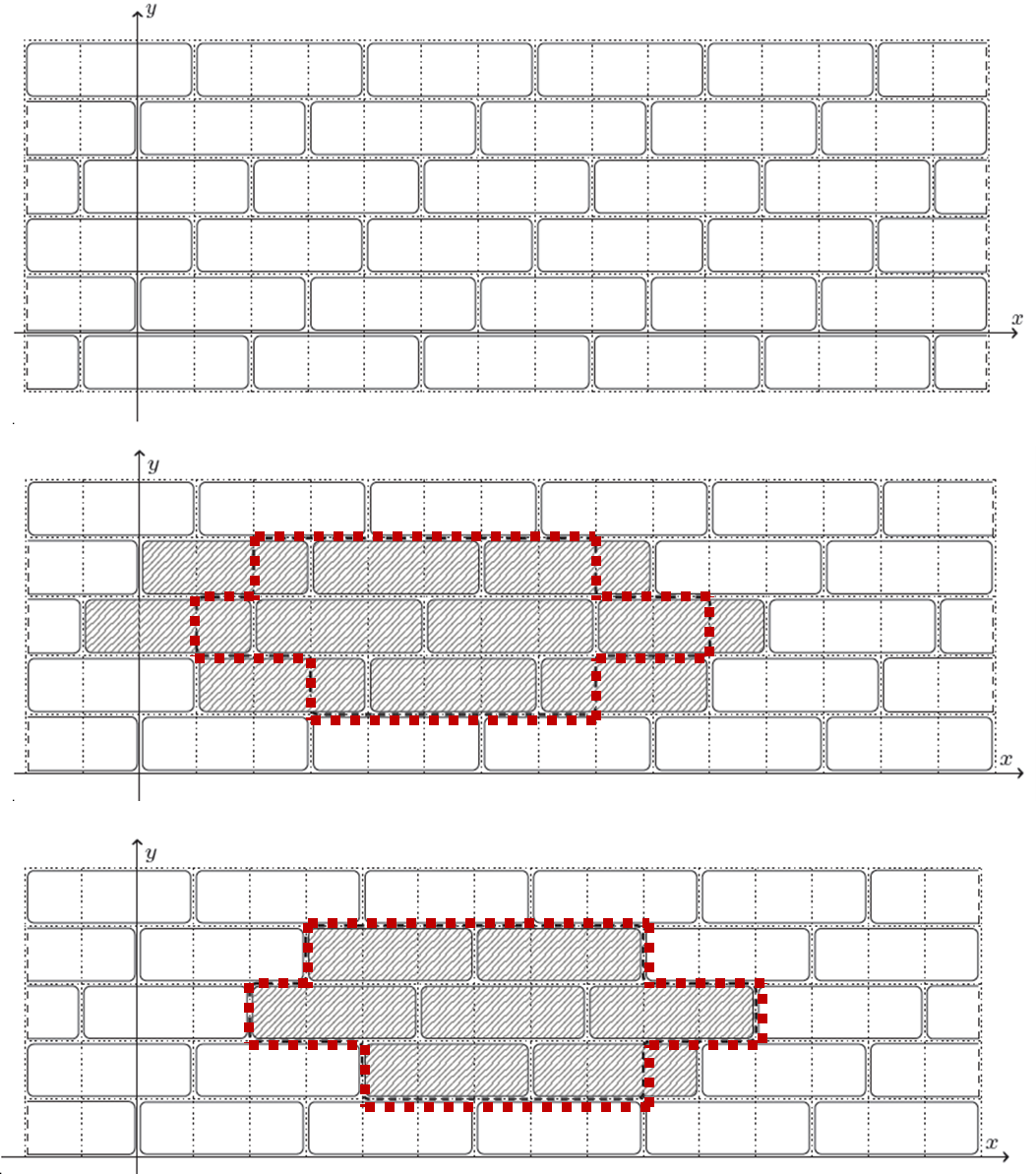
Quảng trường trung tâm của thành phố được lát bởi các viên gạch hình chữ nhật kích thước ~1 \times k~, các cạnh luôn song song với hai trục tọa độ. Một viên gạch có đỉnh dưới-trái tại ~(0,0)~. Khi đó, đỉnh dưới-trái của mọi viên gạch có tọa độ dạng ~(i \cdot k + j,; j)~ với mọi số nguyên ~i, j~. (Có thể hiểu: mỗi hàng có hoành độ bị lệch đi ~1~ so với hàng trước.)

Thành phố muốn dựng một tượng đài. Bệ tượng đài là một đa giác đơn gồm ~n~ đỉnh, các cạnh song song với trục tọa độ, các đỉnh có tọa độ nguyên. Ngoài ra đa giác thỏa tính chất: với mọi đường thẳng song song trục tọa độ, nếu đường đó cắt phần bên trong của bệ thì tập giao điểm bên trong tạo thành một đoạn thẳng (không bị tách rời).

Để xây bệ, người ta phải bóc bỏ mọi viên gạch bị bệ đè lên (dù chỉ một phần). Để giảm số gạch cần bóc, thành phố cho phép tịnh tiến bệ song song với các trục tọa độ (cộng cùng một ~dx~ vào mọi hoành độ và cùng một ~dy~ vào mọi tung độ). Hãy tìm số viên gạch tối thiểu phải bóc.

Yêu cầu

Tìm giá trị nhỏ nhất của số viên gạch có phần giao không rỗng với bệ tượng đài sau khi được tịnh tiến bởi một vectơ ~(dx,dy)~ song song với các trục tọa độ.

Dữ liệu

• Dòng đầu: hai số nguyên ~n~ và ~k~.
• ~n~ dòng tiếp theo: dòng thứ ~i~ chứa hai số nguyên ~x_i, y_i~ là tọa độ đỉnh thứ ~i~ của đa giác. Các đỉnh được liệt kê theo thứ tự ngược chiều kim đồng hồ.

Kết quả

In ra một số nguyên: số lượng tối thiểu các viên gạch cần bóc.

Ví dụ

Ví dụ 1

Input

12 3
2 3
1 3
1 2
3 2
3 1
8 1
8 2
10 2
10 3
8 3
8 4
2 4

Output

7

Ràng buộc

• ~1 \le n, k \le 10^5~
• ~0 \le x_i, y_i \le 10^6~
• Đa giác có các cạnh song song trục tọa độ, đỉnh nguyên, liệt kê ngược chiều kim đồng hồ.
• Với mọi đường thẳng song song trục tọa độ, nếu cắt phần trong của đa giác thì giao là một đoạn thẳng.