Các bàn trong lớp được xếp thành một hàng dọc. Mỗi bàn có 2 vị trí ngồi: vị trí bên trái được đánh số ~1~, vị trí bên phải được đánh số ~2~. Lớp có ~n~ học sinh nên có đúng ~n~ vị trí được sử dụng (tức là xét ~n~ vị trí đầu tiên theo thứ tự phát đề).

Hôm nay có ~k~ đề kiểm tra khác nhau, được phát theo thứ tự sau:

• Bắt đầu từ bàn ~1~ vị trí ~1~, rồi bàn ~1~ vị trí ~2~,
• tiếp theo bàn ~2~ vị trí ~1~, rồi bàn ~2~ vị trí ~2~, …
• Cứ phát lần lượt đề ~1~, đề ~2~, …, đề ~k~, rồi quay lại đề ~1~, đề ~2~, … cho đến khi tất cả ~n~ học sinh đều nhận được đề.

Alice đến trước và ngồi ở bàn ~p~, vị trí ~q~.

Bob đến sau và muốn chọn một vị trí ngồi sao cho:

• Bob nhận được cùng đề với Alice,
• Bàn Bob ngồi có chỉ số gần bàn ~p~ nhất (tức là tối thiểu ~|u - p|~),

• Nếu có nhiều cách có cùng khoảng cách nhỏ nhất, Bob sẽ chọn bàn ở phía trước Alice, tức là có ~u~ nhỏ hơn.

  

Nếu không tồn tại vị trí nào (khác Alice) để Bob thỏa mãn yêu cầu thì in ra ~-1~.

Yêu cầu

Hãy xác định bàn ~u~ và vị trí ~v~ mà Bob cần ngồi. Nếu không có cách, in ra ~-1~.

Dữ liệu

• Dòng 1: số nguyên ~n~ (~2 \le n \le 10^9~)
• Dòng 2: số nguyên ~k~ (~2 \le k \le n~)
• Dòng 3: số nguyên ~p~ (~1 \le p \le (n+1)/2~)
• Dòng 4: số nguyên ~q~ (~1 \le q \le 2~)

Kết quả

• Nếu không có cách ngồi thỏa mãn, in ra:

-1

• Nếu có, in ra một dòng gồm hai số nguyên ~u~ và ~v~.

Ví dụ

Ví dụ 1

Input

25
2
1
2

Output

2 2

Giải thích

Ví dụ 1

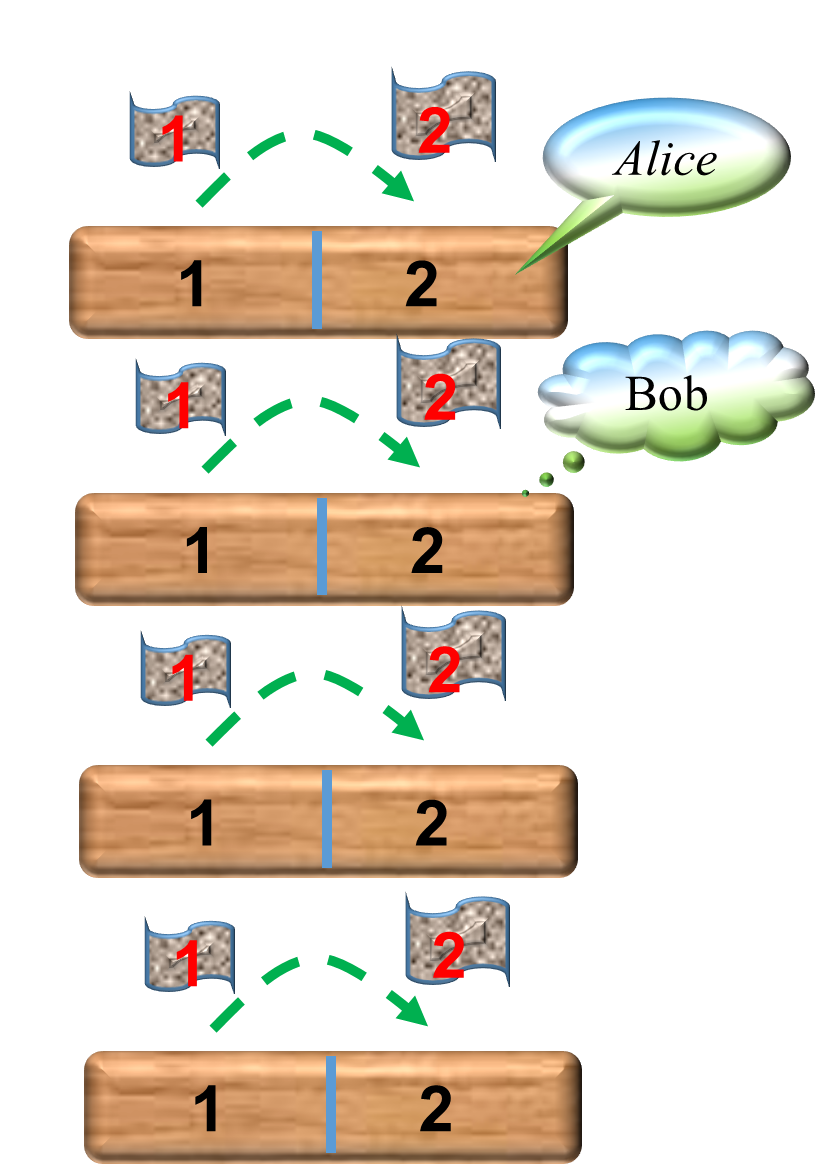
Thứ tự phát đề theo các vị trí là ~1,2,1,2,1,2,\dots~ (vì ~k=2~). Alice ở bàn ~1~ vị trí ~2~ nên nhận đề ~2~. Vị trí gần nhất khác Alice cũng nhận đề ~2~ là bàn ~2~ vị trí ~2~.

Ràng buộc và chấm điểm

Ràng buộc

• ~2 \le n \le 10^9~
• ~2 \le k \le n~
• ~1 \le p \le (n+1)/2~
• ~1 \le q \le 2~